Presentation
A Hybrid Factorization Solver with Mixed Precision Arithmetic for Sparse Matrices
SessionResearch Posters Display
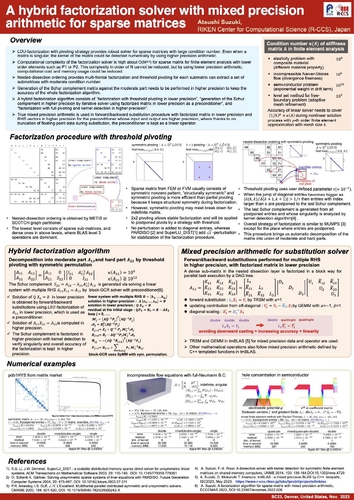
DescriptionFor numerical simulations, linear system with large sparse matrix with high condition number needs to be solved. LDU-factorization with pivoting strategy provides robust solver for such system. Computational complexity of the factorization solver is high and cannot be reduced in framework of the direct solver, but by using lower precision arithmetic, computational cost and memory usage could be reduced. LDU-factorization uses recursive generation of the Schur complement matrix, but generation of the last one can be replaced by an iterative method. Here decomposition of the whole matrix into a union of the moderate and hard parts during factorization with threshold pivoting plays a key role. A new algorithm uses factorization in lower precision as a preconditioner for iterative solver in higher precision to generate the last Schur complement. True mixed precision arithmetic is used in forward/backward substitution for preconditioner with factorized matrix in lower precision and RHS vectors in higher.
Event Type
Posters
Research Posters
TimeTuesday, 14 November 202310am - 5pm MST
LocationDEF Concourse
TP
XO/EX
Archive
view
